Teaching Geometry From Every Angle
Geometry instruction at the Washington Waldorf School takes the same shape as that of all our subjects. Our methods build a deep understanding of the subject matter, giving students the skills they will need for college while also encouraging exploration and critical thinking — skills they will need no matter which path they follow.
At Waldorf, we build a solid foundation in the fundamentals and nurture capacities necessary for future learning before moving to the next level.
We also employ “horizontal integration,” reinforcing learning by incorporating overlapping elements from subjects such as science, math, history, and art into all of our courses. And we’re keenly sensitive to students’ unique needs at different ages, so courses are tailored to where students are in their development.
In the early grades, we teach math through direct experience. At those ages, children learn math best in visual, tangible, and concrete ways, so our students experience the subject through movement, drawing, stories, and puzzles, and by manipulating, touching, and counting objects. This builds a firm understanding for the learning that follows in students’ later years, as children progress to solving math problems in more abstract ways.
Problem-solving and practical applications of math are a constant theme in all grades. As students move to the higher grades, we teach them to think critically and challenge assumptions.
Building a Strong Foundation

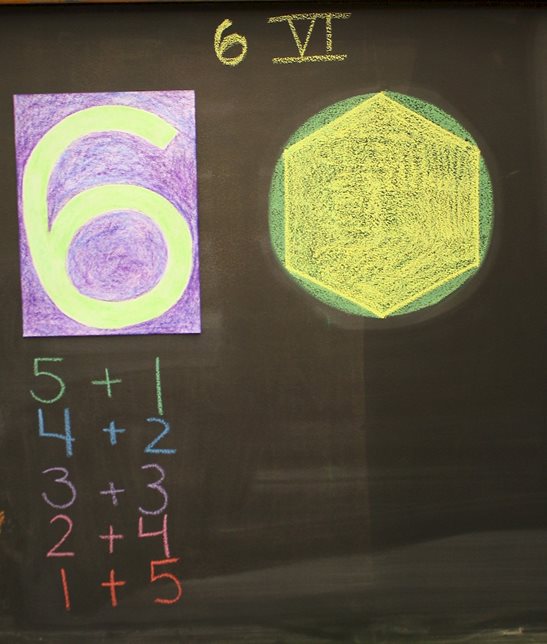
Here’s how this approach applies for geometry.
Geometry instruction begins in first grade and is integrated into the students’ introduction to addition, subtraction, division, and multiplication. We do this so our students can begin to make connections between numbers and shapes. For example, when learning about the number 6, students write Arabic and Roman numerals, draw hexagons, and place a hexagon in a circle they’ve drawn. First-graders also are introduced to the idea of factoring and fractions in geometry: In one such lesson, they divide a circle (representing the number 1) in half, discovering that they can create two halves from one shape.
The connection between shapes and numbers continues through the lower grades. In second or third grade, students may use string to connect six points on a circle to create a hexagon, two triangles, and a six-pointed star (hexagram). The teacher may suggest that they consider the numerical relationship between a triangle and a hexagram. Children can make all sorts of discoveries with this approach, forming foundations for learning about fractions in fourth grade or about algebra in seventh grade.
Freehand drawing of different geometric shapes and figures — such as circles, spirals, multisided forms, and right angles — helps children make connections too. They may note the number and length of the sides of shapes they draw. We don’t tell them a square has four equal sides and that a rectangle has two pairs of equal sides; they learn on their own through creating.

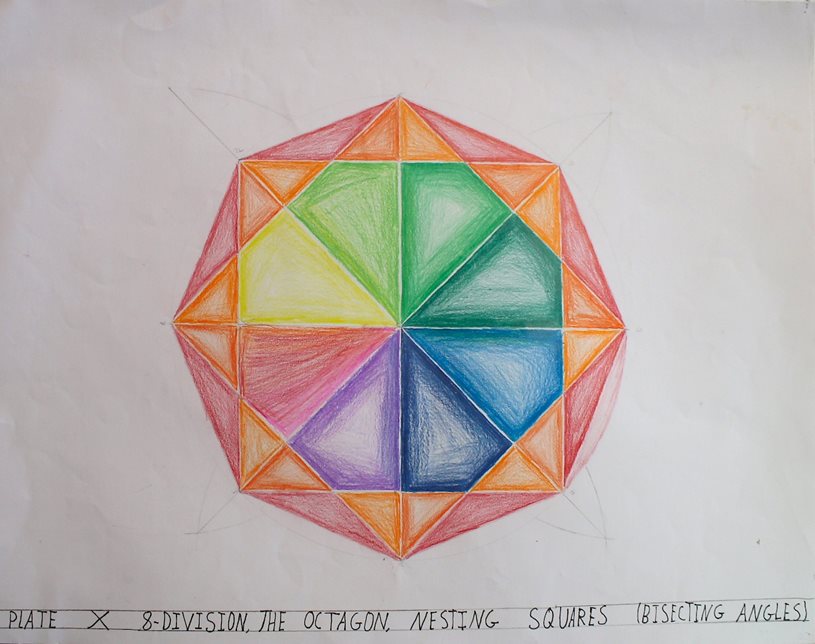

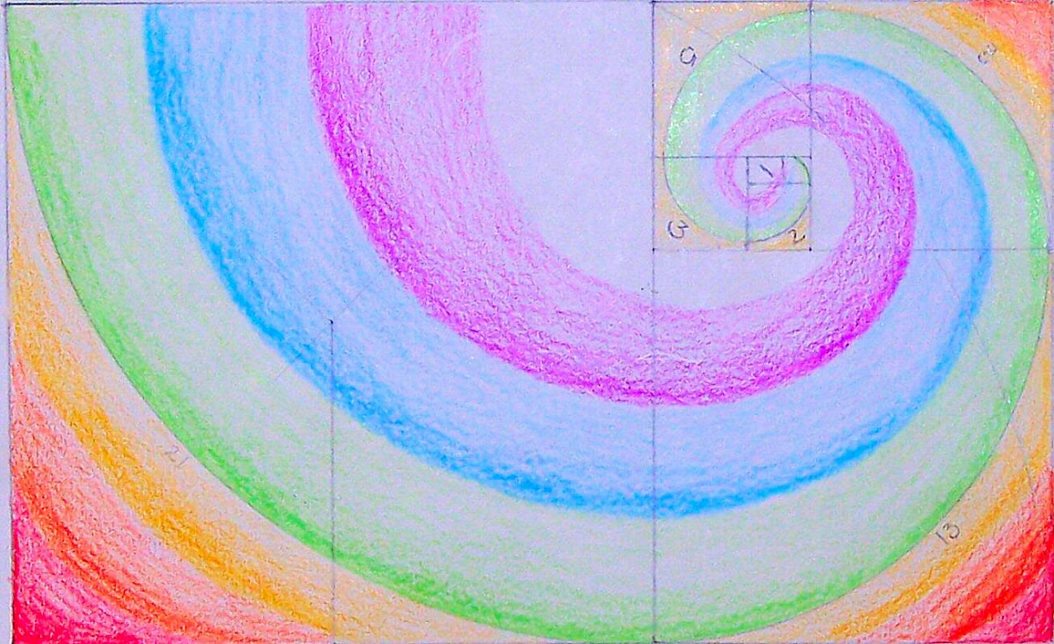
Fifth-grade botany brings attention to shapes and forms in flowers, plant stems, and other natural elements. In the seventh and eighth grades, students again observe the way leaves grow in a spiral around the stem of a plant when they learn about the Fibonacci sequence — a series of numbers in which any number is the sum of the two numbers that came before it; the pattern appears regularly in nature
By sixth grade, students are ready to be introduced to a higher level of precision through geometric drawing. Using compasses and straightedges — a direct and tactile method that reinforces students’ learning before they use computers in our high school classrooms — they create exact drawings and begin exploring geometric principles, equations, and proofs. Each discovery builds a stronger foundation in geometry and skills — including logic — that are essential for solving a wide range of problems.
In Eurythmy classes, which involve expressive movement, students may walk or run in geometric formations like a triangle or star. In one exercise, 12 students form a circle, and then one student — using yarn in different colors — connects every other student, then every three, every four, and every six students, until the yarn forms a hexagon, square, triangle, and line.
History and geometry are intertwined in upper-elementary and middle school math.
When fifth-graders study the ancient Egyptians, the students discover geometry’s practical application. Using ancient methods and tools for measurement, such as ropes knotted at regular intervals, students make angles and shapes to re-create how the Egyptians divided land and built pyramids.
CHALLENGING ASSUMPTIONS
After a full year of geometry in 10th grade, 11th-graders turn once again to their compasses and straightedges to explore projective geometry, taught in a four-week block of daily 95-minute sessions. Eleventh-grade students also receive a full year of instruction in subjects like algebra and trigonometry.
Until 11th grade, Waldorf students learn Euclidean geometry — the study of flat space in which, for example, parallel lines never intersect. Euclidean geometry, the kind we all remember from school, remains an essential building block for learning. The study of non-Euclidean projective geometry, however, calls for students to reject such assumptions and to challenge conventional wisdom.
Returning to our original example, in projective geometry (and other non-Euclidean geometries), parallel lines can and do intersect. This leads to interesting discussions with students about what other geometries are possible, whether the abstract concept of infinity can have tangible properties, and how some of these concepts can be demonstrated with a straightedge and compass. Science, history, philosophy, and art all may be touched on in these conversations.



The study of geometry and of other areas of math builds the problem-solving skills students need to succeed. By the end of high school, each Washington Waldorf School student is prepared for college-level math.
All schools teach geometry, but Waldorf addresses the philosophical aspect of math more consciously than other schools do, illuminating deep questions about truth as well as patterns in nature.
In doing this, our students graduate with a more complete understanding of how geometry and other math concepts apply to the world at large.